So anyone who has done a bit of image processing or machine learning, or both would have heard the term "CNNs". Well, what are they? They are Convolutional Neural Networks. What do they do? They can roughly be described as Neural Networks for images. Why do we need them over regular Neural Networks? This is because they take into account the spatial relation of the pixels, the different color channels as well as being rotation invariant(to a small extent).

So, CNNs are based on mainly one operation - Convolution. What is that exactly?

Convolution

Convolution is an operation, just like addition, subtraction, multiplication, etc. It takes in functions as inputs and technically gives another function as the output. It's a very common operation used in areas like signal processing, image processing, and in our case machine learning, to train neural networks.

So how does it exactly work?

Mathematically, Convolution is defined as:

$$\begin{equation} (f \ast g)(t) = \int_{-\infty}^{\infty} f(\tau) g(t - \tau) \, d\tau \end{equation}$$

Let's break this down:

• Here f and g are the functions that are being convolved.

• 𝜏 is the spatial or temporal variable over which convolution is happening, and is common to both functions.

• The integral stretches over the entire domain of 𝜏, and represents convolution over the entire space or time.

$$y[n] = \sum_{m=-\infty}^{\infty} x[m] h[n-m]$$

This is a discrete approximation of convolution, that is it can be thought of as a sliding window over both functions, where the values of the function in the window are multiplied. Here, y is the output, x is the input and h is the kernel that we are using. Think of them as arrays being indexed by the values in the square brackets. The usage of this formula is more common in practical applications as summing is a simpler operation than integration. This is useful in cases like noise reduction and smoothening as convolution averages out values in the window that we will discuss.

1D Example

For our example, let's take a signal that we want to convolve over:

signal = [1,2,3,4] with the kernel = [1,2,3]

In this visualization, we have reversed the kernel attributed to the minus sign the in equation. The kernel becomes a sliding window, sliding over the input array. As we move the kernel over one element at a time, we will store the product of the respective elements present in the window. This will give our output elements one at a time. The green arrows denote the respective elements being multiplied and the red rectangle indicates the window at that point in time.

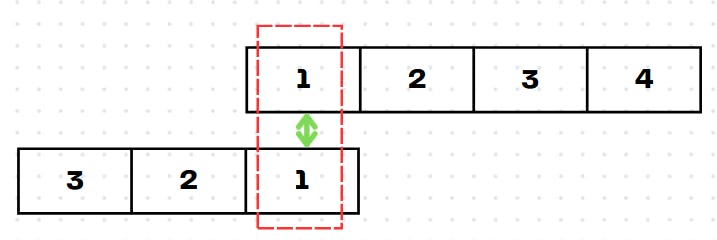
The result is 1*1 = 1

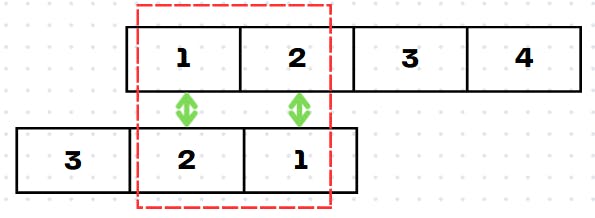
The result is 1*2 + 2*1 = 4

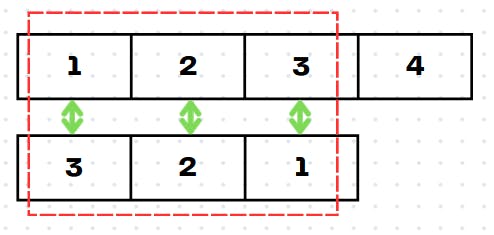
The result is 1*3 + 2*2 + 3*1 = 10

The result is 1*4 + 2*3 + 3*2 = 16

The result is 2*4 + 3*3 = 17

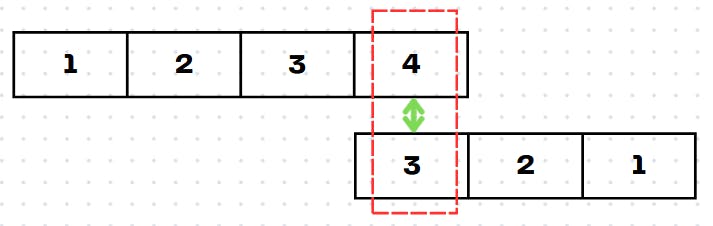
The result is 3*4 = 12

Therefore, our final output is [1, 4, 10, 16, 17, 12]

What about 2D?

In two dimensions, the underlying concept of a sliding window remains the same, however, the movement of the kernel is slightly different. First, for a fixed y = k value, it moves across the x-axis. Then after it's done convolving over the entire x-axis domain, it goes to y = k + 1 and does the same. It keeps going till it traverses the entire domain of y. Now the other thing is that we can customize our convolutions. That is, we can control where the convolutions start from and end from, this will determine the size of the output.

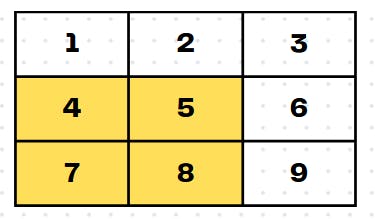
In two dimensions, our input will be a 2D matrix and so will the kernel and the output. We can see the visualization in the example to get a better idea:

The white matrix is the input matrix and the kernel is the yellow matrix. We will move the kernel over the matrix.

We start off from the top-left corner, and we will move the kernel right till we reach the end.

For this element the result is 1*1 + 0*2 + 0*4 + 1*5 = 6

Here, the kernel has reached the end, so we will move it down by one unit.

For this element the result is 1*2 + 0*3 + 0*5 + 1*6 = 8

For this element the result is 1*4 + 0*5 + 0*7 + 1*8 = 12

For this element the result is 1*5 + 0*6 + 0*8 + 1*9 = 14

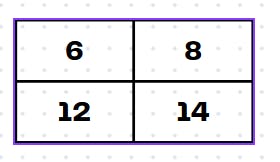
As you can see, this matrix is the convolved output. As you can see, after convolving the input with the kernel, the input got smaller. We can perform different types of convolution based on a few hyperparameters:

• Padding - If we wanted an output matrix of the same size, we can pad the array with zeros, or any other value around the matrix and proceed. Let the amount of padding be P.

• Stride - In our example, we have been moving the kernel by one step, however, we can vary the amount it moves by the stride. The more the stride, the smaller the output will be. Let the stride be S.

• Kernel size - For our example, we have used a kernel size of 2x2. However, we can increase the kernel size to get an even smaller input. Let the kernel size be K.

• Input size - This is the dimension of the input matrix. The bigger the input matrix, the bigger the size of the output. Let the input dimension be W.

We can use the following formula to calculate the dimension of the output:

$$\frac{W-K+2P}{S} + 1$$

This formula is very useful in CNNs, as we can change the way we process information in this way.

3D and above?

As we have seen, 2D convolution is a simple extension of 1D convolution. We can say the same for 3D and above. So for 3D convolution, we can visualize our image and kernels as cubes and move the kernel along the stretch of one axis. For example, first, we can move from one extent of the x-axis to the other. After we finish with that, we move in y-axis by one unit and move along the x-axis similarly. After we finish with the stretch of the y-axis, move one unit along the z-axis. And continue the same way. This can be programmed as nested loops in any language. The following code shows how we can implement a 3D convolution in CPP.

This code can be extended to four dimensions, by adding another layer of nesting:

Conclusion

So this was it about the Convolution operation. There are some more specifics to it, that will be covered later on in the following posts. As you will see later on, convolution is an essential operation to understand, to understand CNNs. Thank you for reading this post. If you have any questions feel free to leave them in the comments.